自己符号化器と Spectral Clusteing の関連性を示した論文
Author
- Fei Tian : http://home.ustc.edu.cn/~tianfei/
- 中国科学技術大学 Ph.D 1年生
- MSRA と共同研究、2014 年に AAAI2 本,COLING1 本を 1st で通してる
Motivation (研究背景・動機)
-
Deep Learning が数多くの応用でめざましい成果をあげている。
-
音声認識
-
画像認識
-
自然言語処理
-
DL において Clustering に関する適切な調査が行われてない。
-
論文の目的として、DL における Clustering の調査を行う
概要
-
Graph Clustering はクラスタリングでも重要な手法の一つ
-
Graph Clustering の応用
-
Image segmentation
-
Community Detection
-
VLSI Design
-
嬉しい点 : ベクトル空間におけるクラスタリングの問題 → データの類似度グラフ問題への変換が可能
-
自己符号化器と Spectral Clustering の類似性
-
Spectral Clustering : グラフラプラシアンに対して EVD を行い k 本の非零固有ベクトルを用いた空間に対して k-means を行ったもの。
-
自己符号化器 : 入力データを低次元化、情報が最大限になるようにデータの次元を再構築する
-
計算量 : 対象とするグラフは n 個のノードを持つ
-
EVD : ナイーブに実装すると O(n3)の計算量、最速の実装は O(n2)の計算量
-
自己符号化器 : ノードがスパースな際は計算量は O(kn)
-
スパース表現 : データが大きくなるならスパース性を有効活用したい
-
EVD : 固有ベクトルが高い確率で密になるため、スパース性が保証されない
-
自己符号化器 : スパース性を用いるのは容易
既存研究で未検証な事柄、何を解決・解明したいのか?
-
Graph Clustering のための Deep Learning の活用方法と調査
-
自己符号化器と Spectral Clustering の類似性とその比較・検証
Method (提案手法)
-
GraphEncoder(for graph clustering.)
-
グラフラプラシアン(L=D−1S)に対してスパース自己符号化器(Sparse-AutoEncoders)を通した最終層に k-meas クラスタリングを行う
-
AutoEncoder は入力層・隠れ層・出力層の 3 層を Stacked する。
-
X(j)=D−1S の列ベクトルを各ユニットに入力し、隠れ層の活性化関数 h(j)を得て、X(j+1)=h(j)と Γ 回(層の階数分)更新する。

Evaluation (検証方法・評価方法・優位性)
-
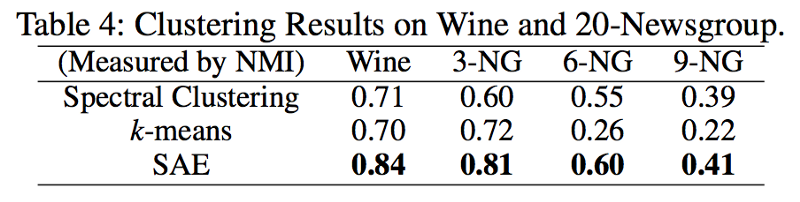
実世界のグラフデータに対して NMI によってクラスタリングの評価実験を行う。
-
データの種類
-
ワイン
-
ニュース記事
-
タンパク質構造グラフ
以下の三種で比較
-
Spectral Clustering
-
k-means
-
Sparse-AutoEncoders(Graph-Encoder)
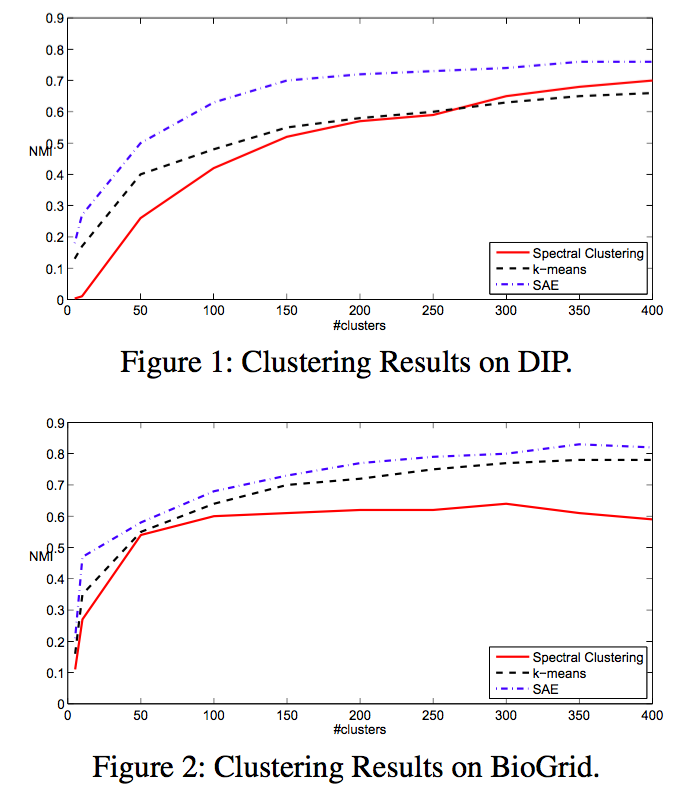
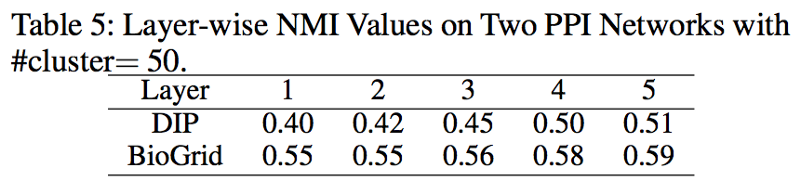
次元の減少推移

層を重ねる毎に NMI が向上している。
Conclusion (結論・貢献)
-
Deep Learn と Graph Clustering の関係性、結果を調査。
-
GraphEncoder の嬉しいところ
-
隠れ層の次元は入力層の次元より低い。これは全てのエッジが必須ではないことを直感的に示す。
-
エッジの除去を行いグラフ表現を更に明確にするために、浅い層から深い層へ。
-
EVD の計算量は最速でも O(n2.367)で、グラフは密なグラフ表現。(Toeplitz Matirix)
-
GraphEncoder は O(ncd)、d は隠れ層の最大次元、c はグラフの平均次元。(例: 各ノードが k 本のエッジを持つ類似度グラフの場合 c=k。ソーシャルグラフで表すと、c は友達の平均の数を示す。)
-
EVD は並列化が困難。確率的勾配降下法(SGD)は EVD と比べると並列化が容易である。
提案手法の限界(残された課題)
実行時間の比較が行われていないが、あくまでこの論文の価値は DL と Graph Clusetering の関連性を示しているのが価値なのでそこは許して下さいって感じ。### Comments (疑問点・わからなかったところ・議論)
-
トップカンファレンスを年 2 本、2nd tier を 1 本 1st で出せるのは、どうやればそのレベルに到達するんだ?
-
トレンドに乗った良い論文。
-
Good Writing. 内容もシンプルなので 90 分でサクッと気持よく読めた。論文読むより、スパース自己符号化の勉強に時間取られた。
-
Corollary2 で ~ symmetrix matrix D−1S って言ってる割に行列の対称性は保証されてないので 3.1 全般が怪しい、辻褄があってない。